Pengertian Matriks Matematika
Halloooo guyss π
Kali ini Saya ingin membahas lanjutan dari Matriks berikut contoh mengerjakannya πππ
Kali ini Saya ingin membahas lanjutan dari Matriks berikut contoh mengerjakannya πππ
Matriks
A. Transformasi Elementer
1. Transformasi Elementer pada Baris dan Kolom Matriks
Terhadap elemen-elemen suatu matriks dapat dilakukan transformasi atau penukaran atau perpindahan menurut baris dan kolom matriks
Berikut kaidah-kaidah transformasi elementer nya guysss :
1. Transformasi Elementer pada Baris dan Kolom Matriks
Terhadap elemen-elemen suatu matriks dapat dilakukan transformasi atau penukaran atau perpindahan menurut baris dan kolom matriks
Berikut kaidah-kaidah transformasi elementer nya guysss :
-Apabila ada matriks A = (aij), maka transformasi elemen-elemen pada baris ke-i dengan baris ke-j ditulis Hij (A), yang merupakan penukaran semua elemen baris ke-i dengan baris ke-j atau baris ke-j dijadikan baris ke-i
Contoh :
-Transformasi elemen-elemen pada kolom ke-i dengan kolom ke-j, ditulis Kij (A), adalah penukaran semua elemen kolom ke-i dengan kolom ke-j atau kolom ke-i dijadikan kolom
ke-j.
ke-j.
Contoh :
- Mengalikan baris ke-i dengan l (l ¹ 0), ditulis Hi(l)(A) dan mengalikan kolom ke-i dengan l ditulis Ki(l)(A).
Contoh :
- Menambah baris ke-i dengan l kali baris ke-j, ditulis Hij(l)(A),Hi + l Hj
Contoh :
- Menambah kolom ke-i dengan l kali kolom ke-j ditulis Kij(l)(A).
Contoh :
- Bila diketahui B adalah matriks transformasi elementer dari A maka matriks A dicari dengan mengambil invers dari matriks B.
Contoh :
2. Matriks Ekivalen
Dua matriks A dan B disebut ekivalen, ditulis A ~ B, jika B diperoleh dari A dengan melakukan transformasi elementer, dan sebaliknya A diperoleh dari B dengan melakukan invers transformasi elementer.
Contoh :
3. Rank Matriks
Rank baris dari matriks A adalah dimensi dari ruang baris matriks A. Rank kolom dari matriks A adalah dimensi dari ruang kolom matriks A. Bila rank baris = rank kolom maka rank matriks A yaitu r (A) adalah harga atau nilai dari rank baris/ rank kolom matriks A tersebut.
contoh :
Secara umum nih guyssss π :
1. Pilih baris / kolom yang bukan vektor nol, dan pilih elemen pada baris/kolom tersebut yang tidak sama dengan nol sebagai elemen pivot. Pada contoh transformasi baris a13 =1 (¹ 0), kemudian pilih baris yang mengandung elemen 1 atau –1 sebagai elemen pivot.
2. Jadikan nol semua elemen yang sekolom dengan elemen pivot melalui transformasi baris oleh elemen pivot tersebut. Pada contoh diatas a23, a33 dan a43 dijadikan nol.
3. Selanjutnya tidak perlu lagi memeperhatikan baris pivot diatas. Perhatikan baris-baris yang tinggal. Pada contoh diatas adalah baris. Kerjakan langkah (1) terhadap mereka. Pada contoh diatas pilih baris 4 dengan elemen pivot a41=1. Seterusnya kembali lagi pada langkah a dan b.
4. Proses ini akan berakhir bila langkah a tidak dapat dikerjakan lagi, yaitu bila telah menjadi baris nol.
B. Determinan
1. Pengertian determinan :
1. Pengertian determinan :
Determinan merupakan sebuah bilangan tunggal atau scalar, dan hanya dijumpai dalam matriks bujur sangkar. Jika determinan suatu matriks bujur sangkar adalah nol, maka matriks tersebut dikatakan sebagai matriks singular.Dan jika determinan matriks tersebut bukan nol, maka matriks tersebut dikatakan sebagai matriks non singular.
Determinan Matriks Ordo 2 x 2
Jika diberikan matriks ordo 2 dinyatakan seperti bentuk di bawah.
A = 
Maka determinan untuk matrik A adalah
Contoh Soal:
Tentukan nilai determinan matriks A =
Pembahasan:
Tentukan nilai determinan matriks A =
Pembahasan:
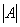= 2.7 - 4.6 = 14 – 24 = - 10Determinan Matriks Ordo 3 x 3
Untuk matriks yang berordo lebih tinggi (matriks 3x3), cara untuk mendapatkan
determinannya adalah dengan cara
Metode Sarrus.
=
Contoh
Sifat-sifat determinan ada enam guysss, yaitu :
1.Determinan suatu matriks sama dengan determinan dari transposenya, det (A) = det(At).
Contoh :
maka Det A = 2.7 – 5.4 = - 6
maka Det At = 2.7 – 4.5 = - 6
2. Penambahan atau pengurangan suatu kelipatan bukan nol dari suatu baris/kolom dari
baris/kolom lainnya tidak akan mempunyai pengaruh pada determinan.
Contoh:
~ H21(-2) (A) → B =
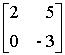
Det B = 2.-3 – 0.5 = - 6
3. Penukaran tempat antara dua baris atau kolom sembarang dari suatu matriks akan
merubah tanda, tetapi tidak merubah harga absolut dari determinan.
4. Determinan dari suatu matriks segitiga (triangular matriks), yaitu matriks dengan
elemen-elemen nol diatas atau di bawah diagonal utama, adalah sama dengan hasil
kali dari elemen-elemen dari diagonal utama.
Contoh:
Contoh:
A=
→ │A│= 1.-2.-1 = 2
→ │A│= 1.-2.-1 = 2
6. Jika dua baris atau kolom identik, atau proporsional, yaitu secara linear tergantung, maka determinan adalah nol.
Contoh
→ │A│= 0
3. Ekspansi Laplace
Metode atau ekspansi Laplace adalah suatu cara untuk menghitung determinan dengan menggunakan kofaktor.
Determinan dari suatu matriks = jumlah perkalian elemen-elemen dari sembarang baris/kolom dengan kofaktor-kofaktornya.
Ekspansi Laplace dapat ditulis dengan cara :
menggunakan baris 1
Dengan pola yang sama dapat juga dihitung dengan menggunakan baris ke dua dan ketiga, dengan memberikan hasil determinan yang sama.
Tanda-tanda kofaktor secara berurutan adalah :
Kofaktor
C11 = (-1)2 M11 = +2 = 2 C21 = (-1)3 M21 = - 4 = - 4
C12 = (-1)3 M12 = -0 = 0 C22 = (-1)4 M22 = +(- 2) = - 2
C13 = (-1)4 M13 = +0 = 0 C23 = (-1)5 M23 = - 0 = 0
C31 = (-1)4 M31 = +(-10) = - 10
C32 = (-1)5 M32 = - 3 = - 3
C33 = (-1)6 M33 = +(-2) = - 2
Sekian pembahasan tentang Matriks berikut contohnya ya guyssss
Terima kasih πππ
Komentar
Posting Komentar